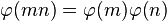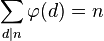티스토리 뷰
ICPC문제를 풀다보면, 결과 값이 중간에 커지기 때문에 modulo값을 구하는 문제가 많이 있다.
modulo값들은 덧셈,곱셈,뺄셈에서는
(A(% p) + B(% p)) % p = (A + B)(% p)
(A(% p) - B(% p) + p) % p = (A - B)(% p)
(A(% p) * B(% p)) %p = (A * B)(% p)
이런식으로 A,B 값을 modulo p를 한 값을 가지고 있으면 (덧셈, 곱셈, 뺄셈) 값을 구할 수 있다.
하지만 나누기의 경우
(A(% p) / B(% p)) % p != (A / B)(% p)이다. 그렇기 때문에 계산 전 값을 가지고 있어야하고,
그 값이 Integer를 넘는다면.. 큰수 계산을 해야한다면... 굉장히 힘들 것이다.
그렇기 때문에 Fermat's little theorem. Euler's theorem. 나 (Extended Euclidean algorithm을 이용할 수 있다. -> 잘모름)
이때, B 와 P가 서로소여야만 한다. GCD(B,P) = 1. (greatest common divisor)
Fermat's little theorem은 P가 소수여야하고,
이다.
이를 양변에 B^2을 나누어주면,

(A(% p) * (1/B)(% p)) % p = (A / B)(% p) 이고, 위 값을 이용하면
(A(% p) * (B^(P-2))(% p)) % p = (A / B)(% p)로 계산 할 수 있다.
이때, B^(P-2) (% p)를 For문을 P-2번 반복하며 만들지 말고,
B(%p), B*B(%p), B*B*B*B(%p)를 바로 구하는 것 처럼 제곱을 이용해서 빠르게 구한다.
그러면 나눗셈이 포함된 modulo 계산에서도 쉽게 할 수 있다.
Euler theorem은 위 상황에서 P가 소수가 아니라면
φ(p) : 오일러 파이 함수. ( 1부터 n까지 양의 정수중 p 과 서로소인 것의 갯수).
를 이용하여 위와 같은 방법으로 구하면된다.
이때 p가 소수라면. Fermat's little theorem이 된다.
오일러 파이 함수를 구하는 방법 :
일반적으로,  는 곱셈적 함수다. 즉, m, n이 서로소인 정수일 때,
는 곱셈적 함수다. 즉, m, n이 서로소인 정수일 때,
이다.
임의의 수의 약수들의 파이 함수값들의 합은 원래 수와 같다. 이 공식은 레온하르트 오일러가 증명하였다.
만약 a와 n이 서로소이고 n이 자연수이면 다음이 성립한다. 이를 오일러의 정리라고 한다.
만약 어떤 수의 소인수들을 안다면, 그 오일러 파이 함수는 다음과 같이 계산할 수 있다. 이 공식을 오일러 곱 공식(영어: Euler product formula)이라고 한다.
참고 ) https://ko.wikipedia.org/wiki/오일러의_정리 , https://ko.wikipedia.org/wiki/오일러_피_함수
- Total
- Today
- Yesterday
- 책 소개
- ROS2
- 창숨김 프로그램
- 창숨기기 프로그램
- iptime 2000au
- 2000au
- readonly
- USB
- ubuntu
- 블로그
- 디스크 쓰기 금지되어 있습니다
- C 책
- 창숨김
- ROS2 설치
- C#책
- c#.net
- C# 책
- robot
- Node
- C#입문
- C# 속으루..
- 블로그 개설
- ipTIME
- 블로그 이야기
- c#ㄱㄱ
- c#
- c#초보
- 블로그 공지
- 창숨기기
- 창숨김 다운
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 |